Ribbon Curves

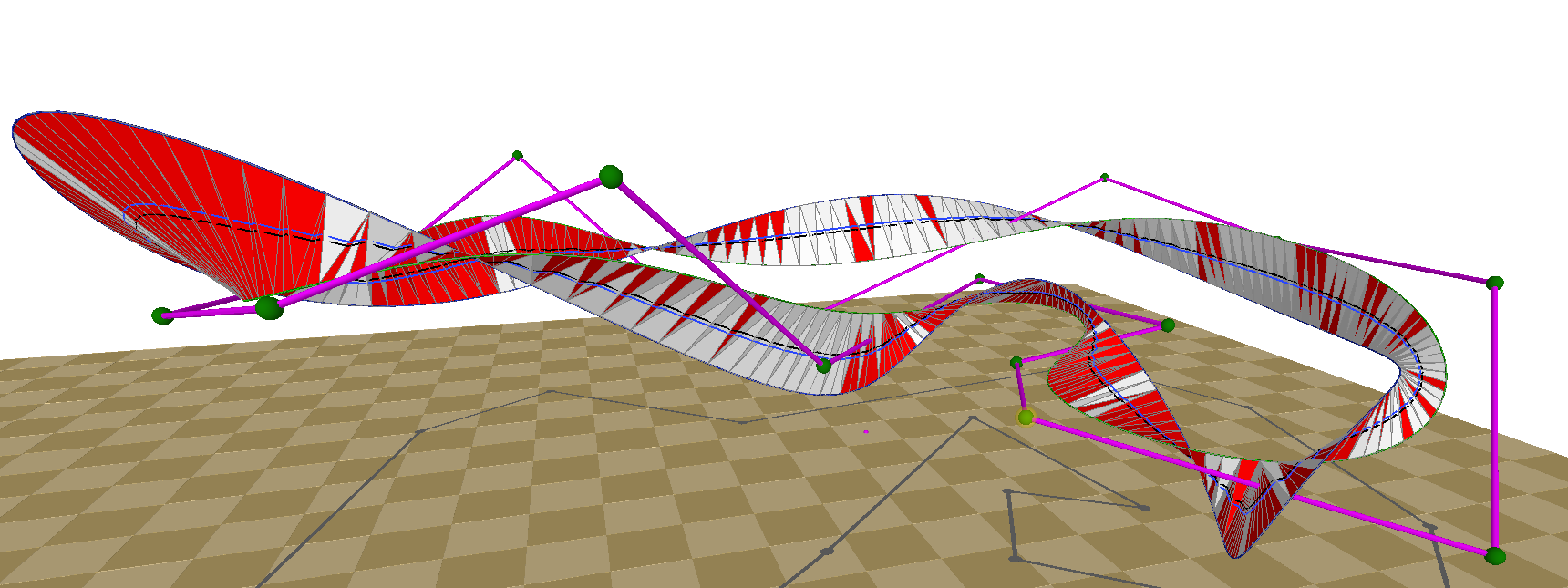
Project 3 for Foundation of Computer Graphics was to use two curves in 3D space to create a pipe with a bonus aspect for coming up with a symmetric solution for the pipe or being able to show an osculating ball that would roll along one curve while not ever being pierced by the other. In addition to performance improvements from using OpenGL display lists, I came up with what may be an original solution to the problem by way of what I call the wrapping paper or ribbon method for continuously mapping one curve onto the other. The process starts with discretized versions of the curves and the two points from each curve that are closest to one another across all points. The process then marches along the curves point by point creating triangles by selecting the shorter of the next two edge candidates. This results in a ribbon between the curves that is then used for finding a more stable mid-point mapping between the curves than other solutions that only consider the absolute closest point of the other curve regardless of context. This also produces a symmetric solution that does not depend on which curve is the basis for solving the problem.